School of Engineering, The University of Tokyo* Japan Synchrotron Radiation Research Institute** Graduate School of Frontier Sciences, The University of Tokyo*** Photon Factory, KEK****
○Kouhei Okitsu* Yoshitaka Yoda** Yasuhiko Imai** Yoshinori Ueji*** XiaoWei Zhang****
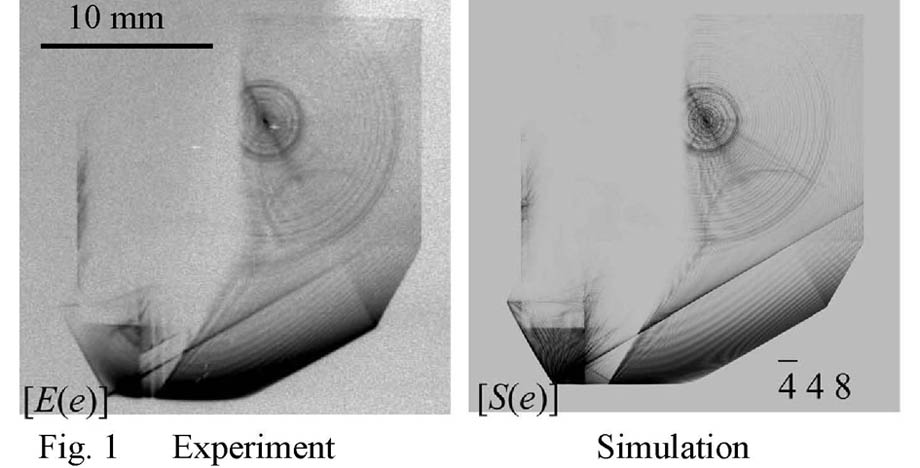
The Takagi-Taupin equation has been extended to n-beam cases (Okitsu, K (2003). Acta Cryst. A59, 235-244.) where n is 3, 4, 5, 6, 8 or 12, taking into account the polarization effect, correctly. A new algorithm numerically to solve the new theory has also been developed. X-ray six-beam pinhole topographs with a parallel-sided floating zone silicon crystal have been experimentally obtained with the incidence of X-rays whose polarization state was controlled by using a 'four-quadrant phase retarder system' (Okitsu, K. et al. (2002). Acta Cryst. A58, 146-154.). They agreed quantitatively with computer-simulated images using the new algorithm based on the new theory (Okitsu, K. et al. (2006). Acta Cryst. A62, 237-247.). Figure. 1 shows -4 4 8-reflected images of experimentally obtained and computer-simulated six-beam pinhole topographs with a channel-cut floating zone silicon crystal, which reveals that the new theory and algorithm can calculate correctly an n-beam wave field excited in a crystal with an arbitrary shape. The polarization state of X-rays for Fig. 1 was left-screwed circular. A further advanced n-beam Takagi-Taupin equation and an algorithm to solve it that are applicable to arbitrary number of n will also be mentioned.
